PRS 계산의 Concept은 아래와 같다.

PRS는 Risk allele들의 합산 score로 계산되는데, 해당 SNP의 Weight인 effect size가 가장 중요하다.
이 Beta distribution을 어떻게 추정하는지가 오늘의 주제다.
미리 결론부터 말하자면 PGS Catalogue에 등재된 PGS 있다면 그대로 사용하는 것을 권한다.
이러한 방법으로는 크게 C-T (Clumping + Thresholding), Shrinkage, Bayesian approach로 나누어진다.
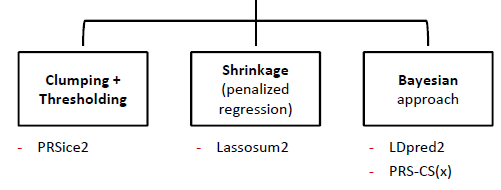
1. C-T : PRSice2
C-T든 P-T(Pruning)는 모두 LD relationship을 고려해서 가장 관계된 SNP만을 선택하는 과정이다.
Threshold의 경우 best-fit PRS를 제공하기 위해 많은 p-value threshold에서 PRS를 계산한다.
effect size의 경우 GWAS summary statistics를 사용한다.
Genotyped (PLINK Format) data, Imputed (BGEN Format - VCF) data 모두 사용 가능
Available at https://github.com/choishingwan/PRSice

**Clumping은 유전적 연관성이 높은 SNP들 중에서 가장 낮은 p-value를 가진 SNP을 기준으로 주변의 상관관계가 높은 SNP들을 제거. Pruning은 SNP 간의 상관계수(보통 r² 값)를 사용해 일정 기준(예: r² > 0.2) 이상으로 상관된 SNP들을 제거하고, 남은 SNP들은 분석에 사용. Clumping은 유의미한 SNP 중에서 대표적인 하나를 선택하는 것이 목표인 반면, Pruning은 전체 데이터셋에서 중복된 정보를 줄여 분석의 효율성을 높이는 데 중점을 둔다.
분석을 하고 나면 PRS의 quantile에 따른 phenotype에 대한 odd ratio를 나타내는 Quantile plot을 얻을 수 있다.

2. Shrinkage (Penalized Regression) : Lassosum2
Lassosum2의 기본 concept는 이름에서와 같이 LASSO이고, X가 여러 개인 다중 선형 회귀 모형에서 overfitting 되는 경우가 발생할 때 덜 중요한 X에 대한 가중치를 제거하고자 하는 것이다. (제약 조건 : Lasso, Ridge)
Lassosum2는 공개된 데이터(예: 요약 통계 데이터베이스)를 사용하여 SNP 간의 상관관계(𝑅)와 SNP와 표현형 간의 상관관계(𝑟)를 추정하는데, 참조 패널로 사용된 유전자형 데이터와 차이가 있을 수 있다는 문제점이 있다.
pseudo-correlation이라는 특징도 있다. summary statistics 데이터는 SNP와 질병 간의 연관성을 나타내지만, SNP 간의 상관관계는 포함하지 않는 경우가 많다. 따라서 연구자는 직접 상관관계를 계산할 수 없는 상황에 처할 수 있는데, 이때 주로 t-통계량과 상관관계 간의 단조(monotonic) 관계를 이용해 p-value를 상관관계로 변환한다.
* t-통계량 : 회귀 분석에서 회귀 계수의 유의성을 평가하는 지표. 일반적으로 t-통계량의 절댓값이 2 이상이면, 해당 계수가 유의미하다고 판단. 정규분포 2SD를 생각하면 된다.
LDpred2와 같은 input data 사용. R package bigsnpr
** Lasso, Ridge ChatGPT
Lasso (L1 norm)는 회귀 계수들의 절댓값 합에 페널티를 부과, Ridge (L2 norm)는 제곱합에 페널티를 부과. Lasso 회귀는 L1 정규화를 사용하여 일부 계수를 0으로 만듭니다. Ridge 회귀는 L2 정규화를 사용하여 모든 계수를 줄이지만, 그 값을 0으로 만들지는 않습니다. 이는 제곱합에 패널티를 부과하기 때문에 발생하며, 모든 변수를 모델에 남겨두게 됩니다.
이러한 특성 때문에 Lasso는 중요한 변수를 선택하는 데 유용하고, Ridge는 모든 변수의 기여를 균등하게 조절할 때 유용
*** Penalized 는 penalty를 받는 것. 단어를 잘 보자.
3. Bayesian approach :
- 1. LDpred2

Bayesian approach에서 effect size에 대한 사전분포는 point-normal mixture distribution을 따른다고 가정하는데, 효과 크기(𝛽)는 특정 비율로 실제로 유전적 효과가 존재하는 SNP와 그렇지 않은 SNP로 나누어진다. 유전적 효과가 존재한다면 특정 평균과 분산을 따를 것이고, 그렇지 않다면 effecdt size는 0이 된다. 이 사전분포는 후에 GWAS marginal effect의 영향을 받아 사후분포를 따르게 된다. (수식 생략)
LDpred2의 특징으로는 long-range LD region에서 causal variant에서 high predictive performance를 보인다는 것과 특정 염색체에서 역할을 더 잘 할 수 있다는 것이다. (예를 들어, 6번 염색체는 인간 면역 체계와 관련된 주요 조직 적합성 복합체(MHC)를 포함하고 있어, 자가면역 질환과 연관된 변이들이 많이 존재할 수 있는데 이렇게 특정 염색체에만 특이적인 형질 분석시 도움이 된다.)
필요한 Data는 Lassosum2와 동일하다. (GWAS summary statistics, LD matrix-R[상관계수], Tuning hyper-parameters, Validation set)
Available at R package bigsnpr https://privefl.github.io/bigsnpr/
** Bayesian 모델은 Bayesian 확률론에 기반하여 사전 정보(prior)와 데이터를 결합하여 사후 분포(posterior distribution)를 추정하는 방법이다.
*** Hyper-parameter들은 모델을 학습시키는 과정에서 최적의 값을 찾아내기 위해 반복적으로 조정되며, 이를 통해 모델의 예측 성능을 최대화한다. Cross-validation이 이 과정에서 쓰이는데, 데이터를 n개의 fold로 나눈 뒤 n번의 test를 거쳐 모델의 적합성을 평가하는 방법이다.
- 2. PRS-CS
Bayesian regression framework and continuous shrinkage (CS) prior on SNP effect sizes.
특히, LD 구조를 고려하여 SNP 간의 상관관계를 반영한 블록 업데이트 방식이 효과적.
sample 크기가 작고 유전적 구조가 희소한 경우 성능이 떨어질 수 있다. (100K - 1000 causal SNPs 일 때 prediction >> 10k - 100 causal SNPs)
LD reference panel이 제공된다.

- 3. Cross-population prediction; PRS-CSx
Trans-ancestry population을 연구하는 방법은 크게 세 가지다.
(1) Meta (PT-meta): GWAS summary statistics를 두 집단 간의 유전적 구조 차이나 LD 차이를 고려하지 않고 단순 결합만.
(2) Multi (PT, LDpred2, PRS-CS): 각 인구 집단에서 별도로 PRS를 계산한 다음, 이들을 선형 결합하여 최종 PRS를 만든다. 이는 각 인구 집단의 고유한 특성을 반영하지만, 공유된 유전적 구조를 고려하지 않습니다.
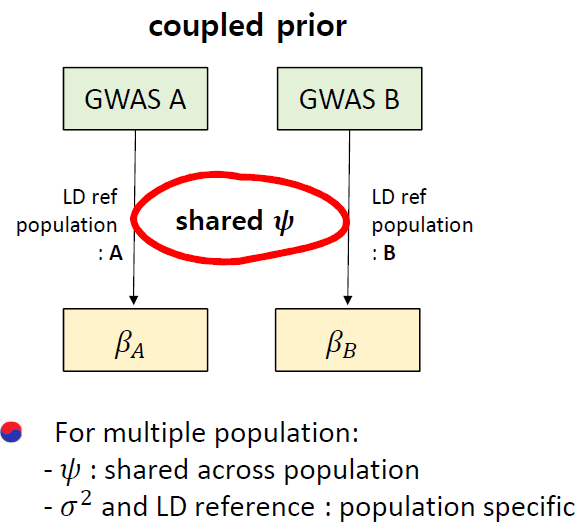
(3) Coupled Prior (PRS-CSx): 각 인구 집단 간에 공유된 유전적 구조(예: 𝜓)를 모델링하여 PRS를 계산합니다. 각 인구 집단의 특이한 effect size의 크기와 LD 구조도 함께 고려.
### 새로운 PRS Weighting 값 만들고 싶다면
C-T, LDpred2( + Lassosum2), PRS-CS(x) 권장, 이후 PRS 전체 분포 확인하고 Performance (대표적으로 AUROC, R^2)를 비교해서 사용한다.
Ref. 2024년도 GENESIS-K 유전체 강의
'GENETICS' 카테고리의 다른 글
| Mendelian Randomization - Essential for study design (2) | 2024.09.20 |
|---|---|
| LD Block 에 대해 (0) | 2024.09.12 |
| GWAS의 Application (3) (0) | 2024.08.24 |
| GWAS 의 전반적 과정 (2) (0) | 2024.08.22 |
| GWAS - 전장 유전체 분석 Introduction (1) (0) | 2024.08.18 |




댓글